Elementos característicos de la elipse
Hay varios elementos, como por ejemplo
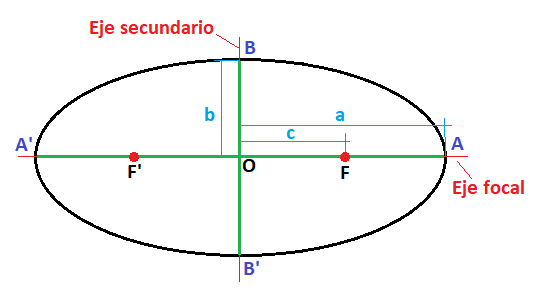
Loa focos, los vértices. Como podemos observar en esta imagen.
La fórmula de este triángulo rectángulo es:
a^2= b^2+ c^ 2
7.1^2 = 5`2 + 5`2
da aproximadamente los dos 50 cm
La ecuación de la elipse es:
x^2/ a^2 + y^2/ b^2= 1
Hay dos tipos de focos, el foco y el foco prima. Estos focos son simétricos si los podemos medir en la vida real. Para saber la distancia focal de esta es sumar el foco, y el foco prima y dividirlo entre dos.
Supongamos que la distancia focal sea 10 cm entonces dividimos 10 entre 2 que es igual a 5 cm.
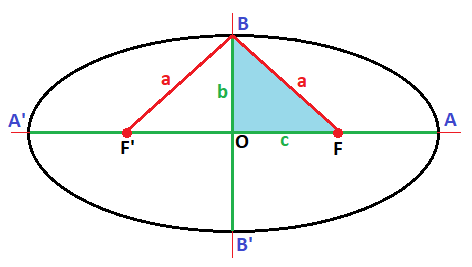
El parámetro característico de esta fórmula es c. Esta seria la fórmula. C= d(f f´) / 2 Los vértices son unos puntos de corte con los ejes de coordenadas los que sobresalen en rojo en la imagen que tenemos arriba. A, A´, B, B´. Estos ejes son simétricos. A,A´= 7.1 CM, cada una ,lo que indica que son simétricos. B, B´= 5 CM cada una, lo que indican que son simétricos. d( A,A´)= eje mayor = 14.2 CM. 14.2= 2a. a es el parámetro característico. A= 7.1cm. d(B,B´)= eje menor = 10 CM. 10=2b. b es el parámetro característico. B= 5cm. ¿Qué cumple cualquier elemento de la elipse? La suma de los radios vectores es igual al eje mayor. Radio vector: distancia del punto a cada uno de los focos. ¿Que relación hay entre los parámetros a,b,c? La relación que hay en estos parámetros es el triangulo rectángulo que podemos observar en esta imagen.
a^2= b^2+ c^ 2
7.1^2 = 5`2 + 5`2
da aproximadamente los dos 50 cm
La ecuación de la elipse es:
x^2/ a^2 + y^2/ b^2= 1
Comentarios
Publicar un comentario